
Chủ đề lối trung tuyến tam giác cân: Đường trung tuyến tam giác cân nặng không chỉ có là 1 định nghĩa cơ phiên bản nhập hình học tập, nhưng mà còn là một khóa xe nhằm giải quyết và xử lý nhiều yếu tố tương quan cho tới tính đối xứng và cân đối trong những dạng tam giác. Bài ghi chép này tiếp tục khiến cho bạn nắm rõ rộng lớn về đặc thù và phần mềm thực tiễn của lối trung tuyến nhập tam giác cân nặng, một dụng cụ luôn luôn phải có cho tới những ai yêu thương quí toán học tập.
Bạn đang xem: tính chất đường trung tuyến trong tam giác cân
Tính hóa học của lối trung tuyến nhập tam giác cân
Đường trung tuyến nhập tam giác cân nặng là đoạn trực tiếp kẻ kể từ đỉnh (đỉnh của góc cân) cho tới trung điểm của cạnh lòng. Đường trung tuyến này còn có những đặc thù quan trọng như sau:
- Đường trung tuyến vuông góc với cạnh lòng và phân tách tam giác trở nên nhị tam giác nhỏ với diện tích S cân nhau.
- Đường trung tuyến cũng chính là lối cao và lối phân giác của tam giác.
Độ lâu năm lối trung tuyến ứng với cạnh a được xem theo gót công thức:
Trong đó:
- ma: Độ lâu năm lối trung tuyến ứng với cạnh a.
- a, b, c: Độ lâu năm những cạnh của tam giác.
Trọng tâm của tam giác là vấn đề uỷ thác nhau của tía lối trung tuyến và cơ hội từng đỉnh một khoảng chừng vày 2/3 chừng lâu năm lối trung tuyến trải qua đỉnh ê.
| Tỉ lệKhoảng cơ hội kể từ trọng tâm cho tới những đỉnh | G - A2/3 ma | G - B2/3 mb | G - C2/3 mc |
Xét tam giác ABC cân nặng bên trên A, chừng lâu năm cạnh lòng BC là 12 centimet, chừng lâu năm lối trung tuyến AM kể từ A cho tới trung điểm M của BC là 8 cm:
- Áp dụng công thức, tao với AM là lối cao, lối phân giác bên cạnh đó là lối trung tuyến.
- Do AM vuông góc với BC nên tam giác ABM và tam giác ACM là nhị tam giác vuông với diện tích S cân nhau.
Những đặc thù này canh ty tất cả chúng ta nắm rõ rộng lớn về quan hệ trong số những nhân tố nhập tam giác và là nền tảng cho những vấn đề tương quan cho tới tam giác nhập hình học tập.
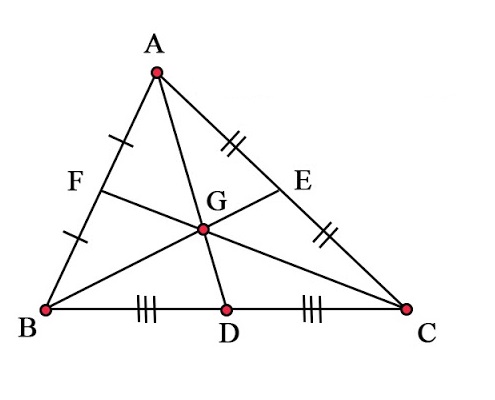
Giới thiệu cộng đồng về lối trung tuyến nhập tam giác cân
Đường trung tuyến nhập tam giác cân nặng là 1 định nghĩa cần thiết nhập hình học tập, với tầm quan trọng không chỉ có nhập lý thuyết mà còn phải nhập phần mềm thực tiễn. Đường trung tuyến được khái niệm là đoạn trực tiếp kẻ từ là một đỉnh của tam giác và phân tách song cạnh đối lập.
Tam giác cân nặng là dạng tam giác nhưng mà nhị cạnh mặt mày có tính lâu năm cân nhau. Trong tam giác cân nặng, lối trung tuyến kẻ kể từ đỉnh đối lập với cạnh lòng không chỉ có là trung tuyến nhưng mà còn là một lối cao và lối phân giác, điều này thực hiện cho tới nó trở thành quan trọng rộng lớn đối với những loại tam giác không giống.
- Tính chất: Đường trung tuyến phân tách tam giác trở nên nhị tam giác nhỏ cân nhau về diện tích S.
- Ứng dụng: Đường trung tuyến canh ty xác lập trọng tâm của tam giác, là vấn đề cân đối hình học tập hoàn toàn có thể phần mềm nhập nghệ thuật và kiến thiết.
Dưới đấy là một số trong những điểm nổi trội về lối trung tuyến nhập tam giác cân:
- Đường trung tuyến canh ty phân loại tam giác một cơ hội đối xứng.
- Nó là dụng cụ hữu ích trong những công việc thi công và đo lường nhập nghệ thuật.
- Trong thực hành thực tế đo lường khu đất đai, lối trung tuyến canh ty xác lập những điểm số lượng giới hạn một cơ hội đúng mực.
| Tính ChấtMô Tả | Đường CaoĐường trung tuyến kẻ kể từ đỉnh cũng chính là lối cao nhập tam giác cân nặng. | Đường Phân GiácĐường trung tuyến kẻ kể từ đỉnh cũng phân giác góc ở đỉnh. | Trọng TâmĐiểm bắt gặp của tía lối trung tuyến là trọng tâm, phân tách từng lối trung tuyến trở nên tỷ trọng 2:1. |
Định nghĩa và đặc thù của lối trung tuyến nhập tam giác cân
Đường trung tuyến của một tam giác cân nặng được khái niệm là đoạn trực tiếp chuồn từ là một đỉnh của tam giác và kết đôn đốc bên trên điểm thân thích của cạnh đối lập. Trong tam giác cân nặng, nhất là lối trung tuyến kể từ đỉnh cân nặng xuống cạnh lòng, nó còn là một lối cao và lối phân giác của tam giác ê.
Sau đấy là một số trong những đặc thù chủ yếu của lối trung tuyến nhập tam giác cân:
- Đường trung tuyến phân tách tam giác trở nên nhị tam giác nhỏ với diện tích S cân nhau.
- Nó là lối phân giác của góc bên trên đỉnh, phân tách góc ê trở nên nhị góc cân nhau.
- Là lối cao của tam giác, nó vuông góc với cạnh đối lập bên trên điểm ở chính giữa.
Biểu thao diễn toán học tập của đặc thù lối trung tuyến:
| Tính ChấtCông Thức | Chiều lâu năm lối trung tuyến$$ m = \frac{1}{2} \sqrt{2b^2 + 2c^2 - a^2} $$ | Phân phân tách diện tíchDiện tích nhị tam giác nhỏ là cân nhau. |
Như vậy, lối trung tuyến không chỉ có tăng thêm ý nghĩa nhập lý thuyết hình học tập nhưng mà còn là một dụng cụ hữu ích trong những vấn đề thực tiễn, canh ty đơn giản đo lường và phân loại những hình phức tạp trở nên những phần giản dị và đơn giản rộng lớn.
Công thức tính chừng lâu năm lối trung tuyến nhập tam giác cân
Trong tam giác cân nặng, lối trung tuyến không chỉ có là 1 đường thẳng liền mạch giản đơn nhưng mà còn là một lối cao và lối phân giác nếu như kẻ kể từ đỉnh. Vấn đề này được chấp nhận tất cả chúng ta vận dụng một công thức quan trọng nhằm tính chừng lâu năm lối trung tuyến, quan trọng Lúc nó bắt nguồn từ đỉnh và trở lại cạnh lòng.
Giả sử tao với tam giác cân nặng bên trên A, với chừng lâu năm cạnh lòng là b, và chừng lâu năm nhị cạnh mặt mày là a. Đường trung tuyến kể từ A cho tới cạnh lòng BC cũng chính là lối cao và lối phân giác của tam giác.
- Công thức tính chừng lâu năm lối trung tuyến, m, kể từ đỉnh A xuống cạnh lòng BC là:
$$ m = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} $$
Phân tích công thức:
- Chia cạnh lòng BC trở nên nhị nửa cân nhau, từng nửa có tính lâu năm là $$ \frac{b}{2} $$.
- Áp dụng toan lý Pythagoras nhập tam giác vuông tạo ra vày lối trung tuyến m, nửa cạnh lòng $$ \frac{b}{2} $$ và cạnh mặt mày a, tao hoàn toàn có thể tìm kiếm được chừng lâu năm của m.
- Điều này canh ty xác lập chừng đúng mực cao trong những vấn đề tương quan cho tới đo lường nghệ thuật và kiến thiết hình học tập.
Bằng việc dùng công thức này, người tao hoàn toàn có thể đơn giản đo lường và vận dụng nhập nhiều trường hợp thực tiễn, kể từ ê giải quyết và xử lý những vấn đề phức tạp một cơ hội hiệu suất cao.
Xem thêm: đô thị hóa là một quá trình
Trọng tâm tam giác và côn trùng tương tác với lối trung tuyến
Trọng tâm của tam giác, còn được gọi là tâm barycenter, là vấn đề uỷ thác nhau của tía lối trung tuyến của tam giác. Điểm này còn có đặc thù cần thiết về mặt mày hình học tập và là trọng tâm của tam giác, điểm cân đối phân bổ lượng của tam giác nếu như fake sử nó là 1 vật thể với tỷ lệ tương đồng.
Trong tam giác cân nặng, trọng tâm với những điểm sáng khác biệt sau:
- Trọng tâm phân tách từng lối trung tuyến trở nên nhị phần, phần dài thêm hơn gấp hai phần ngắn thêm, và phía trên đoạn trực tiếp nối kể từ đỉnh cho tới trung điểm của cạnh đối lập.
- Trong tam giác cân nặng, trọng tâm luôn luôn phía trên lối cao, lối trung tuyến và lối phân giác bắt nguồn từ đỉnh cân nặng.
Công thức toán học tập cho tới địa điểm của trọng tâm nhập tam giác, gọi là G, hoàn toàn có thể được xác lập như sau:
$$ G = \left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right) $$
trong ê xi và yi là tọa chừng của những đỉnh tam giác.
- Khi xác xác định trí trọng tâm, tao cần thiết đo lường tầm nằm trong của tọa chừng những đỉnh.
- Trọng tâm hoàn toàn có thể được dùng nhằm xác lập trung điểm của những quy tắc toán hình học tập phức tạp, canh ty giản dị và đơn giản hóa những vấn đề tương quan cho tới tam giác.
Việc nắm rõ về trọng tâm và côn trùng tương tác của chính nó với lối trung tuyến không chỉ có tiện ích nhập hình học tập mà còn phải trong tương đối nhiều nghành nghề dịch vụ khác ví như nghệ thuật, kiến thiết và phân tích khoa học tập.
Ứng dụng của lối trung tuyến nhập giải toán thực tế
Đường trung tuyến của tam giác không chỉ có là 1 định nghĩa cơ phiên bản nhập hình học tập nhưng mà còn tồn tại nhiều phần mềm cần thiết nhập thực tiễn đưa, nhất là trong những nghành nghề dịch vụ như nghệ thuật, kiến thiết và phân tách tài liệu.
Dưới đấy là một số trong những phần mềm rõ ràng của lối trung tuyến nhập giải toán thực tế:
- Xác toan trọng tâm: Đường trung tuyến canh ty lần trọng tâm của tam giác, điểm nhưng mà bên trên ê tía lối trung tuyến bắt gặp nhau, với phần mềm nhập cân đối cấu hình và kiến thiết quy mô.
- Tối ưu hóa thiết kế: Trong kiến thiết cơ khí và phong cách xây dựng, lối trung tuyến được dùng nhằm đáp ứng đối xứng và cân đối, canh ty tối ưu hóa chức năng của những cấu hình.
- Phân tích và giải những vấn đề phức tạp: Trong những vấn đề tương quan cho tới tối ưu và phân tách, lối trung tuyến canh ty giản dị và đơn giản hóa và giảm sút những đổi mới số, thực hiện rõ rệt quan hệ trong số những nhân tố của vấn đề.
Ngoài rời khỏi, lối trung tuyến còn tồn tại tầm quan trọng trong:
- Khoa học tập địa hóa học, trong những công việc tế bào phỏng và đo lường trọng tải của những tầng địa hóa học.
- Khoa học tập PC, nhất là nhập nghành nghề dịch vụ hình họa PC và phân tách hình hình ảnh, điểm nó canh ty đo lường những điểm trung gian lận.
- Giáo dục, lối trung tuyến là 1 dụng cụ đào tạo và giảng dạy cơ phiên bản canh ty SV hiểu về đối xứng và cân đối nhập hình học tập.
Với những phần mềm phong phú như thế, lối trung tuyến không chỉ có là 1 dụng cụ lý thuyết mà còn phải là 1 bộ phận chính yếu trong tương đối nhiều toàn cảnh phần mềm thực tiễn.
Ví dụ minh họa dùng lối trung tuyến trong những vấn đề hình học
Đường trung tuyến nhập tam giác cân nặng có tương đối nhiều phần mềm nhập giải những vấn đề hình học tập. Sau đấy là một số trong những ví dụ minh họa:
- Chứng minh tính đối xứng: Trong một tam giác cân nặng, lối trung tuyến kẻ kể từ đỉnh cân nặng xuống cạnh lòng không chỉ có là lối trung tuyến nhưng mà còn là một lối cao và lối phân giác, thực hiện hạ tầng nhằm minh chứng tam giác cân nặng là đối xứng qua chuyện lối trung tuyến này.
- Tính diện tích S tam giác: Sử dụng lối trung tuyến và chừng lâu năm của chính nó, hoàn toàn có thể vận dụng công thức diện tích S tam giác: Diện tích = 0.5 * chừng lâu năm cạnh lòng * chừng lâu năm lối cao (trung tuyến).
- Tối ưu hóa vấn đề tương quan cho tới đo lường cấu trúc: Trong những vấn đề kiến thiết cấu hình, biết địa điểm trọng tâm (giao điểm của những lối trung tuyến) canh ty phân chia trọng tải một cơ hội hiệu suất cao, đáp ứng sự cân đối của cấu hình.
Dưới đấy là một ví dụ cụ thể:
Ví dụ: Cho tam giác ABC cân nặng bên trên A với AB = AC. Gọi M là trung điểm của BC. Kẻ lối trung tuyến AM.
- Chúng tao biết AM là lối trung tuyến, lối cao và lối phân giác của tam giác ABC.
- Xác toan chừng lâu năm AM dựa vào chừng lâu năm của AB và BC dùng công thức Pythagoras:
- $$ AM = \sqrt{AB^2 - \left(\frac{BC}{2}\right)^2} $$
- Tính diện tích S của tam giác ABC dùng lối trung tuyến AM như thể lối cao:
- $$ \text{Area} = \frac{1}{2} \cdot BC \cdot AM $$
Qua ví dụ này, hoàn toàn có thể thấy rằng lối trung tuyến không chỉ có canh ty xác lập những đặc thù của tam giác mà còn phải tương hỗ đo lường diện tích S và những nhân tố tương quan một cơ hội đúng mực.
Chứng minh đặc thù và toan lý tương quan cho tới lối trung tuyến
Đường trung tuyến nhập tam giác với những đặc thù và toan lý cần thiết nhưng mà tất cả chúng ta cần thiết hiểu nhằm dùng bọn chúng một cơ hội hiệu suất cao nhập hình học tập. Sau đấy là minh chứng cho tới một số trong những đặc thù và toan lý cơ phiên bản tương quan cho tới lối trung tuyến nhập tam giác cân nặng.
- Định lý 1: Đường trung tuyến ứng với cạnh lòng của tam giác cân nặng là lối cao.
- Giả sử tam giác ABC cân nặng bên trên A, lối trung tuyến AM xuống cạnh lòng BC.
- Xét tam giác ABC với AB = AC (giả thiết), AM là lối trung tuyến xuống cạnh BC, suy rời khỏi M là trung điểm của BC.
- Do ê, AM phân tách tam giác ABC trở nên nhị tam giác con cái AMB và AMC với AB = AC và MB = MC.
- Từ ê suy rời khỏi tam giác AMB và AMC là tam giác cân nặng bên trên A và M.
- Vì tam giác AMB và AMC cân nặng bên trên A nên góc AMB vày góc AMC.
- Do ê, AM vừa vặn là lối trung tuyến vừa vặn là lối cao.
- $$ \text{Chứng minh hoàn thành.} $$
- Định lý 2: Đường trung tuyến phân tách tam giác trở nên nhị tam giác nhỏ với diện tích S cân nhau.
- Giả sử tam giác ABC với lối trung tuyến AM kể từ A cho tới cạnh BC.
- Đường trung tuyến AM phân tách tam giác ABC trở nên nhị tam giác AMB và AMC.
- Vì M là trung điểm của BC nên MB = MC.
- AM là cạnh cộng đồng của nhị tam giác AMB và AMC.
- Vì vậy, nhị tam giác AMB và AMC với tía nhân tố vày nhau: AB = AC (tam giác cân), AM (cạnh chung), MB = MC (đường trung tuyến).
- Do ê, theo gót toan lý cơ phiên bản nhập hình học tập, diện tích S tam giác AMB vày diện tích S tam giác AMC.
- $$ \text{Chứng minh hoàn thành.} $$
Qua những minh chứng bên trên, tất cả chúng ta hoàn toàn có thể thấy rằng lối trung tuyến không chỉ có là 1 lối giản dị và đơn giản nhập hình học tập mà còn phải đem nhiều đặc thù toán học tập thâm thúy, tương hỗ giải những vấn đề phức tạp rộng lớn.
Các bài xích luyện thực hành thực tế và câu nói. giải chi tiết
Để hiểu sâu sắc rộng lớn về lối trung tuyến nhập tam giác cân nặng và vận dụng nhập giải những vấn đề hình học tập, bên dưới đấy là một số trong những bài xích luyện thực hành thực tế cùng theo với câu nói. giải cụ thể.
- Bài luyện 1: Cho tam giác ABC cân nặng bên trên A, với AB = AC = 5 centimet, BC = 8 centimet. Hãy tính chừng lâu năm lối trung tuyến AM xuống cạnh BC.
- Giải:
- Để tính chừng lâu năm lối trung tuyến AM, tao dùng công thức:
- $$ AM = \sqrt{AB^2 - \left(\frac{BC}{2}\right)^2} $$
- Thay số nhập công thức:
- $$ AM = \sqrt{5^2 - \left(\frac{8}{2}\right)^2} = \sqrt{25 - 16} = 3 \, \text{cm} $$
- Độ lâu năm lối trung tuyến AM kể từ đỉnh A xuống cạnh BC là 3 centimet.
- Bài luyện 2: Tính diện tích S của tam giác ABC ở Bài luyện 1 dùng lối trung tuyến AM như thể lối cao.
- Giải:
- Áp dụng công thức tính diện tích S tam giác lúc biết lối cao:
- $$ \text{Area} = \frac{1}{2} \cdot \text{base} \cdot \text{height} $$
- Trong ê base = BC và height = AM.
- $$ \text{Area} = \frac{1}{2} \cdot 8 \cdot 3 = 12 \, \text{cm}^2 $$
- Diện tích của tam giác ABC là 12 cm².
Những bài xích luyện này không chỉ có canh ty gia tăng kỹ năng về lối trung tuyến mà còn phải tập luyện tài năng giải toán và phần mềm công thức trong những trường hợp thực tiễn.
Xem thêm: nghe thầy thích pháp hòa giảng
Làm thế này nhằm minh chứng rằng lối trung tuyến nhập tam giác cân nặng vuông góc với cạnh cơ sở?
Để minh chứng rằng lối trung tuyến nhập tam giác cân nặng vuông góc với cạnh hạ tầng, tao cần thiết tiến hành quá trình sau:
- Xác toan lối trung tuyến và cạnh hạ tầng của tam giác cân nặng.
- Chứng minh rằng nhị đoạn trực tiếp bên trên lối trung tuyến và cạnh hạ tầng cần thiết minh chứng vuông góc.
- Sử dụng đặc thù của tam giác cân nặng nhằm kiểm soát và điều chỉnh những góc và minh chứng trúng mối quan hệ vuông góc.
Toán 7 - Chương trình mới mẻ - Tính hóa học tía lối trung tuyến của tam giác - Thầy Kenka
Tam giác cân nặng là hình thể đẹp mắt và quan trọng nhập toán học tập. Đường trung tuyến canh ty phân tách song diện tích S và hỗ trợ những quy tắc tính thú vị. Hãy mày mò tức thì bên trên YouTube!
Đường trung tuyến của tam giác | Toán 7 | OLM.VN
olm #sgkmoi #DONGQUY #trungtuyen Bài giảng canh ty những em cầm được: Thế này là lối trung tuyến của tam giác. Tương tác ...












Bình luận