thể tích khối chóp

Thể tích khối chóp là kỹ năng cơ phiên bản tuy nhiên chúng ta học viên lớp 12 cần thiết cầm nhằm học tập chất lượng tốt môn Hình học tập. Những Việc về khối chóp cũng xuất hiện nay thật nhiều trong mỗi bài bác thi đua trung học phổ thông Quốc Gia nên chúng ta cần thiết thám thính hiểu thiệt kỹ và thực hiện bài bác tập luyện thông thường xuyên nhằm nắm rõ kỹ năng. Bài viết lách tại đây tiếp tục share nhiều hơn thế về khối chóp và công thức tính nhanh chóng thể tích của chính nó.

Khái niệm hình chóp và một vài tính chất

Trước khi thám thính hiểu thể tích khối chóp thì quý khách cần thiết thám thính hiểu về hình chóp. Đây là hình dáng học tập bao hàm mặt mày lòng là hình nhiều giác với những mặt mày mặt là hình tam giác đều cộng đồng 1 đỉnh. Đây cũng đó là đỉnh nằm trong hình chóp. Đường cao nhập hình chóp đó là 1 đường thẳng liền mạch hoàn toàn có thể trải qua phần đỉnh và tạo ra một góc vuông với mặt mày lòng. 

Bạn đang xem: thể tích khối chóp

Hiện ni nhì hình dáng chóp thông thường bắt gặp và tên thường gọi tùy theo hình dạng của mặt mày phẳng phiu lòng. Đó là hình chóp tứ giác và hình chóp tam giác. Dường như, hình chóp với một vài đặc điểm tuy nhiên chúng ta cần thiết cầm như sau:

• Hình chóp bao gồm những cạnh mặt mày có tính nhiều năm như nhau thì chân của lối cao nhập hình chóp đó là tâm của lối tròn trĩnh ở nước ngoài tiếp với khá nhiều giác lòng.
• Hình chóp bao gồm những mặt mày mặt nằm trong thiết lập với lòng 1 góc như là nhau thì phần chân của lối cao hình chóp đó là tâm của lối tròn trĩnh ở nội tiếp với khá nhiều giác lòng. 
• Hình chóp bao gồm một mặt mặt mày tạo ra góc vuông với mặt mày lòng thì phần chân của lối cao hình chóp đó là chân của lối vuông góc được vẽ kể từ đỉnh hình chóp xuống bên dưới cạnh lòng nằm trong mặt mày mặt này.
• Hai mặt mày mặt của hình chóp mặt khác vuông góc với mặt mày lòng thì lối phú tuyến của nhì mặt mày mặt này cũng vuông góc với mặt mày lòng.

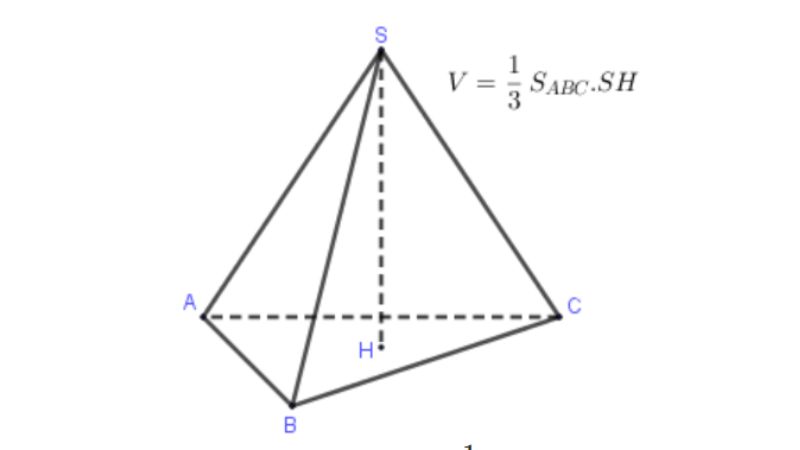
Thể tích hình chóp hiện nay hoàn toàn có thể được xem nhanh chóng với công thức là:

V = 1/3 x S x h. 

Trong đó:

• S: Diện tích của mặt mày phẳng phiu đáy
• h: Chiều cao của hình chóp.

Một số dạng toán tính thể tích khối chóp thông thường bắt gặp và bài bác tập luyện vận dụng

Hiện ni có nhiều dạng toán tương quan cho tới việc tính thể tích của hình chóp vì như thế đấy là hình dáng học tập quan trọng. Sau đấy là một vài dạng toán tính V của hình chóp thông thường bắt gặp kèm theo với những bài bác tập luyện tương quan. Các chúng ta học viên hoàn toàn có thể tham lam khảo:

Dạng toán tính V khối chóp với mặt mày mặt ⊥ với đáy

Để nhận thấy dạng Việc tính thể tích này thì chúng ta cần thiết kiểm tra kỹ khối chóp tuy nhiên Việc thể hiện. Nếu như khối chóp tê liệt với 2 mặt mày mặt mặt khác ⊥ với mặt mày lòng và lối cao hình chóp cũng chính là phú tuyến nằm trong 2 mặt mày vị trí kia thì tất cả chúng ta tiếp tục vận dụng công thức giải này.

Để tính lối cao nằm trong khối chóp thì chúng ta hãy sử dụng quyết định lý như sau:

Để làm rõ rộng lớn về kiểu cách tính V hình chóp này thì chúng ta hãy nhìn qua bài bác tập luyện minh họa như sau: Cho khối chóp S.ABCD bao gồm mặt mày lòng là tam giác ABC vuông ở B, mặt mày phẳng phiu thương hiệu SBC ⊥ với mặt mày phẳng phiu thương hiệu ABC, BC = 4a, BA = 3a. Cho biết góc SBC bởi vì 30 phỏng và SB bởi vì 2a√3. Hãy tính thể tích khối chóp S.ABC.

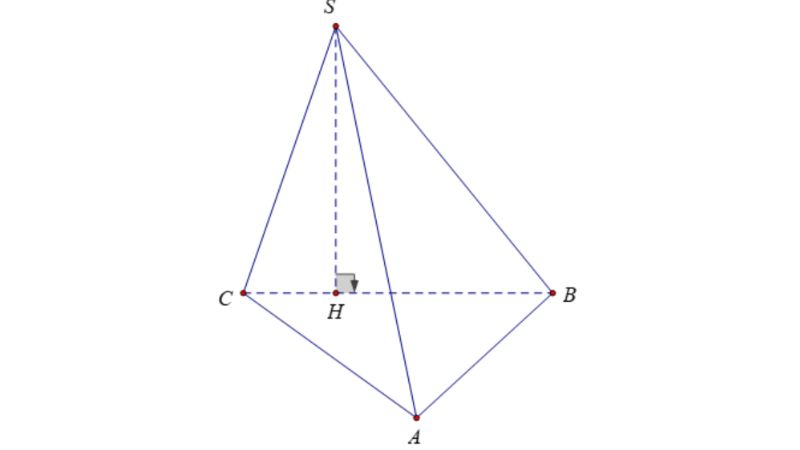
Đáp án:

Bạn hãy kẻ đường thẳng liền mạch SH sao mang lại ⊥ với BC (H cần phía trên cạnh BC). Sau tê liệt tao có: 

• Mặt phẳng phiu SBC ⊥ với mặt mày phẳng phiu ABC
• BC là lối phú tuyến của mặt mày phẳng phiu SBC với mặt mày phẳng phiu ABC
• SH vuông góc với BC
• SH trực thuộc mặt mày phẳng phiu SBC

→ SH vuông góc với mặt mày phẳng phiu ABC

Tiếp cho tới tất cả chúng ta xét cho tới tam giác thương hiệu SHB vuông ở H, tao được:

• SH = SB x sin của góc SBC = 2a√3 x sin30 = a√3
• Diện tích của tam giác ABC = 50% x BA x BC = 50% x 3a x 4a = 6a^2
• Thể tích của hình chóp S.ABC = 1/3 x SH x Diện tích của tam giác ABC = 1/3 x a√3 x 6a^2 = 2a^3√3

Dạng toán tính V khối chóp bao gồm cạnh mặt mày ⊥ với đáy

Như đang được thưa phía trên thì công thức tính V hình chóp bởi vì ⅓ S x h. Mà hình chóp còn tồn tại cạnh mặt mày ⊥ với mặt mày phẳng phiu lòng thì hoàn toàn có thể suy đi ra là cạnh mặt mày này đó là lối cao nằm trong hình chóp với h bởi vì phỏng nhiều năm của cạnh mặt mày ⊥ với lòng. Các chúng ta cũng có thể hiểu rộng lớn về dạng toán tính V hình chóp này qua quýt bài bác tập luyện sau: 

Bài tập: Cho hình chóp thương hiệu S.ABC với cạnh SA ⊥ với lòng, phỏng nhiều năm SA là 4, phỏng nhiều năm AB là 6, phỏng nhiều năm BC là 10 và phỏng nhiều năm CA là 8. Vậy tính V hình chóp S.ABC?

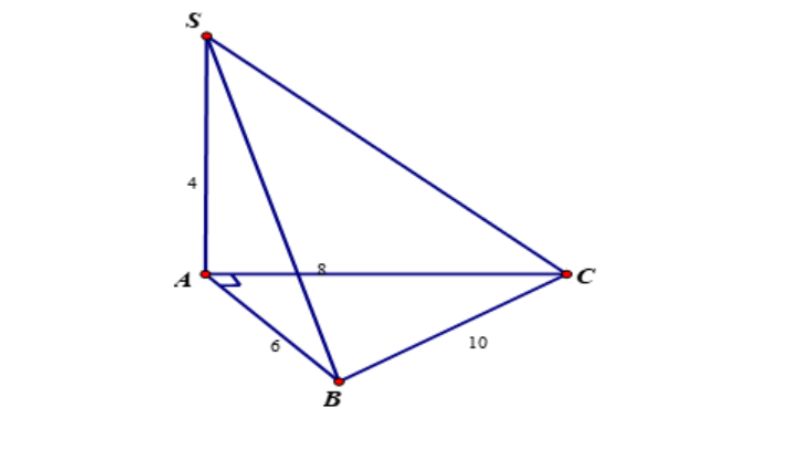
Đáp án:

Ta với AB^2 + AC^2 = 6^2 + 8^2 = BC^2

→ Tam giác ABC với góc vuông ở A.

Vì vậy tuy nhiên diện tích S của tam giác này là: S = 50% AB x AC = 50% x 6 x 8 = 24

Như vậy thể tích khối chóp S.ABC = 1/3 x SA x S của tam giác ABC = 1/3 x 4 x 24 = 32

Dạng toán tính V của hình chóp S.ABCD với lòng là 1 trong những hình vuông

Với dạng toán hình chóp xuất hiện phẳng phiu lòng là 1 trong những hình vuông vắn thì những chúng ta cũng có thể theo đuổi dõi bài bác tập luyện sau:

Bài tập: Cho hình chóp S.ABCD bao gồm mặt mày phẳng phiu lòng là 1 trong những hình vuông vắn với phỏng nhiều năm cạnh là a, cạnh SC thiết lập với mặt mày phẳng phiu SAB 1 góc bởi vì 30 phỏng, cạnh SA ⊥ với lòng. Hãy tính V của khối chóp này?

Đáp án:

• Vì mặt mày phẳng phiu ABCD là 1 trong những hình vuông vắn nên tao với cạnh BC vuông góc với cạnh AB (1).
• Mà cạnh SA lại vuông góc với mặt mày phẳng phiu ABCD nên suy đi ra cạnh SA vuông góc với BC (2).
• Từ (1) và (2), tất cả chúng ta suy đi ra cạnh BC cũng vuông góc với mặt mày phẳng phiu SAB.
• Vì vậy tuy nhiên góc tạo ra bởi vì cạnh SA và mặt mày phẳng phiu SAB = Góc tạo ra bởi vì cạnh SC và SB = Góc CSB = 30 phỏng.
• Từ tê liệt suy đi ra BC/SB = tan30 = √3/3 
• → SB = √3BC = √3a
• Dựa bên trên quyết định lý của Pitago thì cạnh SA = √SB^2 – AB^2 = √3a^2 – a^2 = √2a

Vì vậy tuy nhiên thể tích khối chóp S.ABCD là: 1/3 x SA x S của hình vuông vắn ABCD = 1/3 √a x a^2 = (√2/3) x a^3

Dạng toán tính V hình chóp dạng lập phương 

Đây là hình chóp khá quan trọng vì như thế toàn bộ những mặt mày mặt của hình chóp đều phải sở hữu hình dáng lập phương. Do tê liệt nên phương pháp tính V của hình chóp dạng lập phương này rất giản đơn dàng: V = a x a x a = a^3. Tiếp theo đuổi là một trong những bài bác tập luyện minh họa:

Cho một hình chóp lập phương với lối chéo cánh với phỏng nhiều năm là 27cm. Hãy tính V của hình chóp này?

Đáp án:

Độ nhiều năm những cạnh của hình chóp bên trên là 27/√3 (cm).

Vậy thì V của hình chóp lập phương này bởi vì V = (27/√3)^3 = 6561/√3 (cm^3).

Dạng toán tính V của hình chóp lăng trụ với lòng là tam giác cân nặng đều

Nếu một hình chóp bao hàm mặt mày mặt nằm trong hình dáng bình hành, 2 mặt mày phẳng phiu lòng ở tuy nhiên song và với độ cao thấp như nhau thì nó được nhìn nhận như hình chóp lăng trụ. Nếu hình chóp lăng trụ này bao gồm mặt mày phẳng phiu lòng được nhìn nhận như tam giác cân nặng đều thì nó là hình chóp lăng trụ tam giác cân nặng đều. Sau đấy là bài bác tập luyện nhằm chúng ta làm rõ rộng lớn.

Bài tập: Cho 1 hình lăng trụ là ABC.A’B’C’ xuất hiện phẳng phiu lòng là tam giác đều ABC với cạnh a bởi vì 2cm nằm trong độ cao h bởi vì 3cm. quý khách hãy đo lường thể tích khối chóp lăng trụ này?

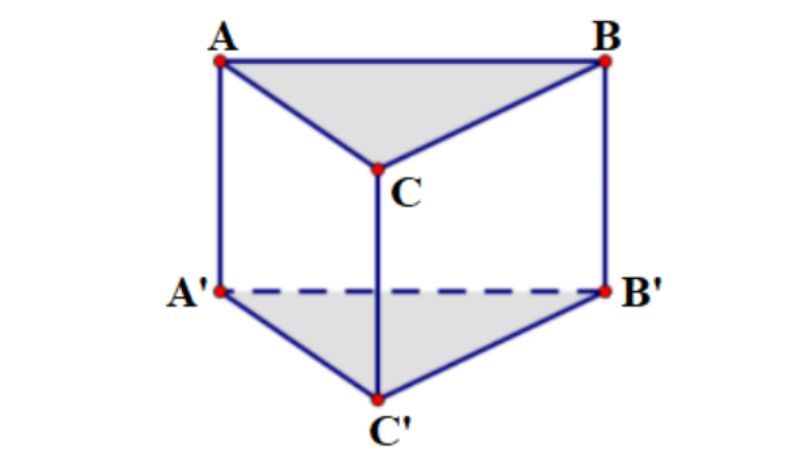
Xem thêm: đóng vai nhân vật bé thu

Đáp án:

Bởi lòng của hình chóp bên trên là tam giác đều phải sở hữu cạnh bởi vì a nên S của tam giác này bởi vì a^2 x √3/4 = 2^2 x (√3/4) = √3 (m2)

Từ tê liệt suy đi ra thể tích của hình chóp lăng trụ này bởi vì S của tam giác ABC x h  = √3 x 3= 3√3 (m3)

Dạng toán tính V của hình chóp với lòng lục giác đều

Để hiểu rộng lớn về kiểu cách tính thể tích hình chóp này thì quý khách coi bài bác tập luyện sau:

Bài tập: Cho 1 hình chóp với lòng là lục giác đều với góc được tạo ra bởi vì cạnh mặt mày nằm trong mặt mày phẳng phiu lòng bởi vì 30 phỏng, phỏng nhiều năm cạnh lòng là a. Hãy tính V hình chóp này?

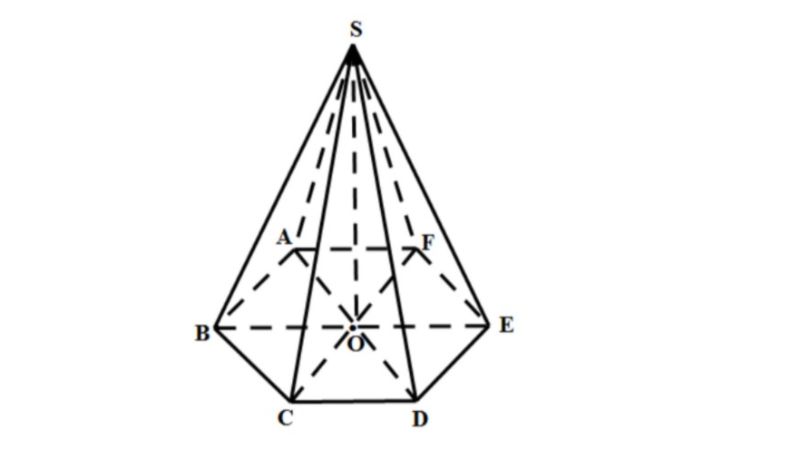
Đáp án: 

Ta gọi thương hiệu của hình chóp phía trên là S.ABCDEF, gọi O là tâm nằm trong mặt mày lòng ABCDEF.

Từ tê liệt suy đi ra OA = OC = OB = OD = OF = OE = AB = CD = BC = DE = FA = EF = a

→ Tam giác OAB là 1 trong những tam giác với những cạnh đều là a.

→ Diện tích của mặt mày lòng ABCDEF vội vàng 6 phiên diện tích S của tam giác OAB. 

→ Diện tích của mặt mày lòng ABCDEF bởi vì (3.a^2.√3)/2

Ta với cạnh SO vuông góc với mặt mày lòng ABCDEF 

→ Góc được tạo ra bởi vì cạnh SA và mặt mày lòng = Góc SAO = 30 độ

→ Cạnh SO = OA x tan30 = (a√3)/3

Như vậy thể tích khối chóp S.ABCDEF = 1/3 x Diện tích của mặt mày lòng ABCDEF x SO = 1/3 x (3.a^2√3)/2 x (a√3)/3 = (a^3)/2

Dạng toán tính V hình chóp bao gồm cạnh mặt mày song một ⊥

Các chúng ta cũng có thể xem thêm bài bác tập luyện sau nhằm thám thính hiểu về kiểu cách tính V hình chóp bao gồm cạnh mặt mày song một vuông góc với nhau:

Cho 1 tứ diện S.ABC bao gồm cạnh SA, SC, SB và song một cạnh mặt mày vuông góc cùng nhau. Cho biết SB = 4a, SA = 3a, SC = 5a. Hãy tính V hình chóp này?

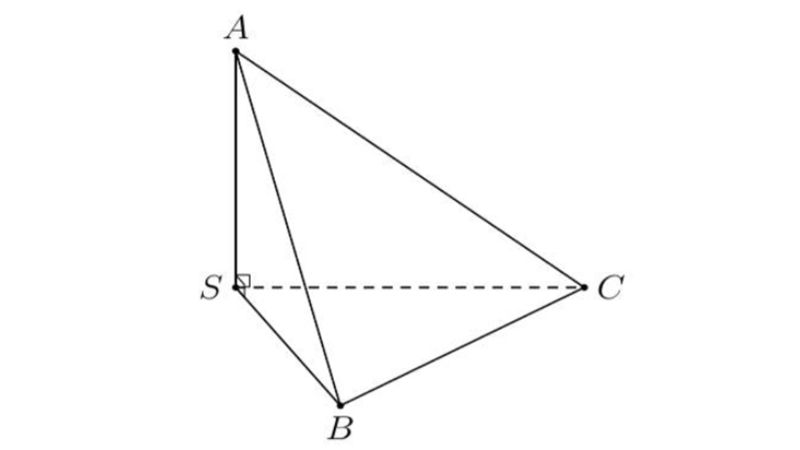
Đáp án:

Ta với cạnh SA vuông góc với cạnh SC, cạnh SA vuông góc với cạnh SB → Cạnh SA vuông góc với mặt mày phẳng phiu SBC.

Từ tê liệt suy đi ra diện tích S của hình chóp tứ diện S.ABC = 1/3 x SA x diện tích S của mặt mày phẳng phiu SBC = 1/6 x SA x SB x SC = 1/6 x 3a x 4a x 5a = 10a^3

Dạng toán tính V hình chóp tròn trĩnh xoay

Công thức tính V hình chóp tròn trĩnh xoay

Công thức nhằm tính V của hình chóp tròn trĩnh xoay tương tự với công thức dùng làm tính V hình chóp cơ bản:

V = 1/3 B x h 

= 1/3 x π x r^2 x h x 1/3 x B x h 

= 1/3 x π x r^2 x h

Trong đó:

• B: Diện tích của lòng với hình dáng nón
• r: Bán kính của mặt mày phẳng phiu lòng với hình nón
• h: Chiều cao hình nón

Bài thói quen V hình chóp tròn trĩnh xoay

Bài tập luyện tại đây tiếp tục khiến cho bạn hiểu rộng lớn về kiểu cách tính thể tích khối chóp tròn trĩnh xoay ở trên:

Cho 1 hình nón cao 2√5 với cùng 1 mặt mày phẳng phiu trải qua phần đỉnh của hình nón rồi tách hình nón này trở nên 1 tiết diện với hình tam giác cạnh đều với S của tam giác = 9√3. Hãy tính V của hình chóp đang được số lượng giới hạn theo như hình nón của đề bài bác.

Đáp án:

Ta với tam giác được tạo ra trở nên kể từ tiết diện là tam giác ABC theo hình sau, điểm I được xem là trung điểm của cạnh BC, coi a như phỏng nhiều năm của cạnh tam giác ABC. Như vậy, tao có:

(a^2√3)/4 = 9√3 → (3a^2)/4 = 27 → AI = a√3 = 3√3

→ OI = √AI^2 – AO^2 = √27 –  trăng tròn = √7

Bán kính của lòng hình dáng nón là R = OC = √OI^2 + IC^2 = √7 + 9 = 4

Xem thêm: tải minecraft 1.18 tiếng việt

Vậy thì V của hình chóp bên trên là V = 1/3 x π x 4^2 x 2√5 = (32√5π)/3 

Nội dung bên trên đang được share không ít công thức tính thể tích khối chóp nhanh gọn mang lại chúng ta thám thính hiểu. Hy vọng những chúng ta cũng có thể giải toán nhanh chóng rộng lớn với những công thức và dạng bài bác tập luyện phía trên. Đây là kỹ năng nền tảng nhằm chúng ta học tập chất lượng tốt rộng lớn môn hình học tập ở bậc trung học phổ thông.

Tham khảo nội dung bài viết liên quan:

• Đường trung tuyến là gì? Tính hóa học, công thức và bài bác thói quen lối trung tuyến
• Công thức lượng giác, bảng công thức lượng giác tương đối đầy đủ nhất